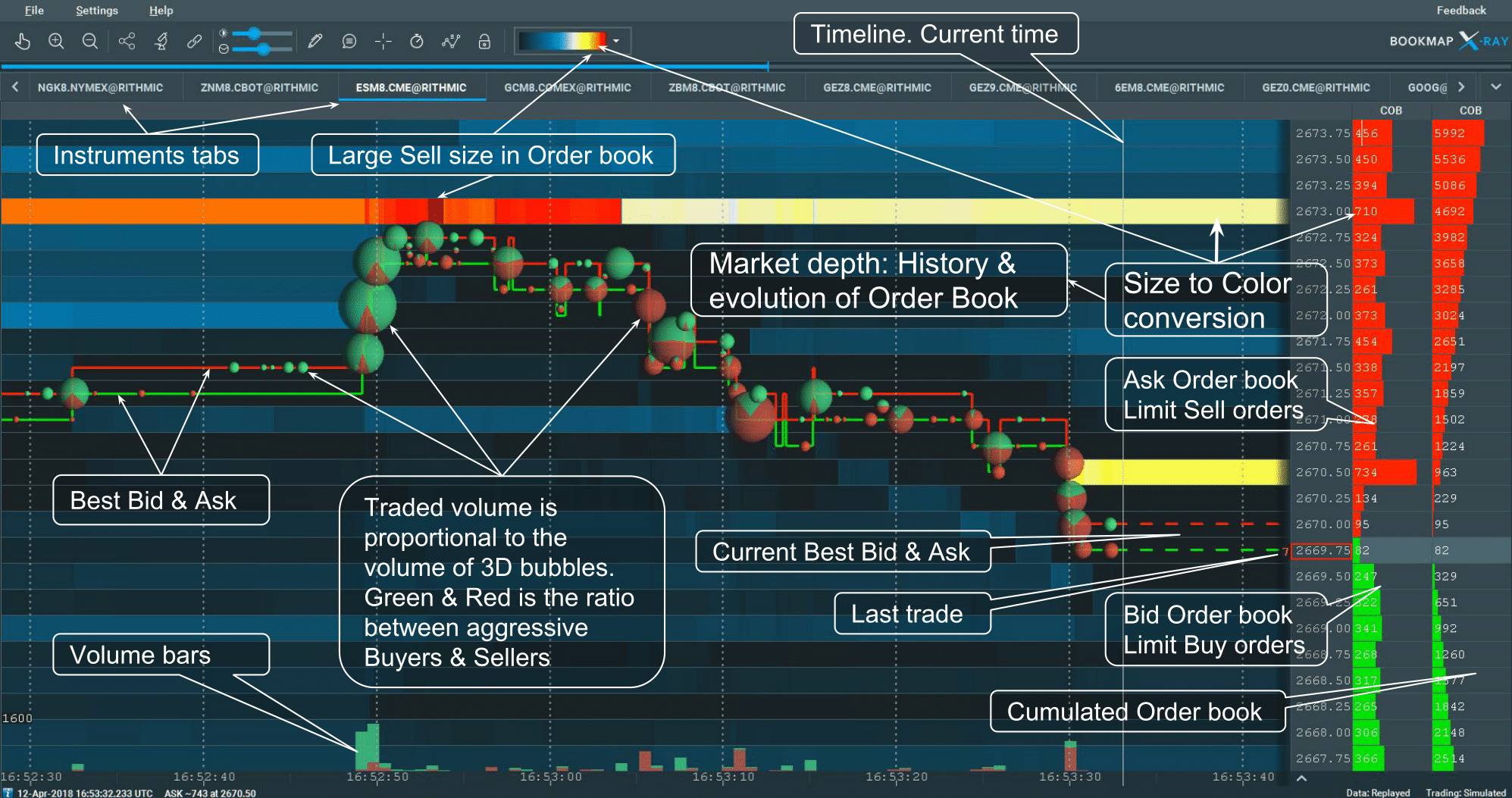
Bookmap Knowledge Base
Welcome to Bookmap, the market depth visualization, and high-speed trading platform. Gain unparalleled insight into equities, futures, and crypto traders' actions and intentions. Our platform empowers informed decisions, competitive advantages, and consistent success through order book and order flow analysis.
The Bookmap Knowledge Base provides essential information to get started, focusing on the Bookmap Alpha version's recent features.
For additional video resources on using Bookmap, visit our Learning Center.